在实际使用中，我们自己编写的fft函数肯定不如专门优化过的库，这里我们使用scipy。

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy import fft

做一下数据准备：

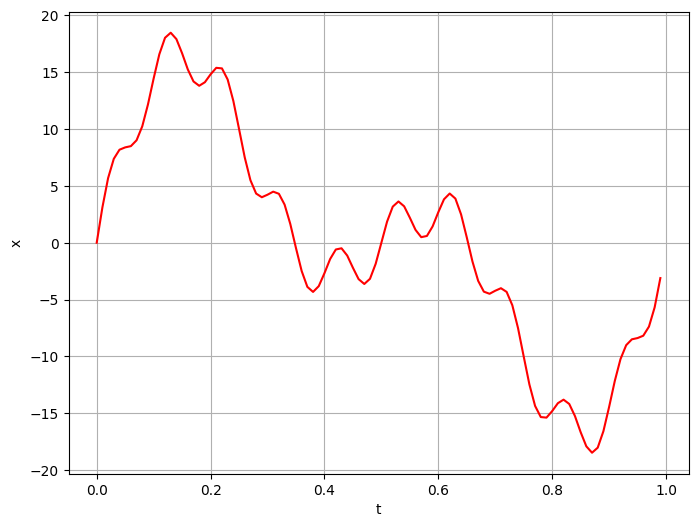
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
rate = 100 # rate 是采样率（每秒采样点数，单位：Hz）
interval = 1 / rate

t_start = 0
t_end = 1
t = np.arange(t_start, t_end, interval) # (0, 1, 1/100)  时间采样

def getSineSignal(amps, freqs, t):  # 接受振幅和频率数组并生成组合信号的函数
    x = np.zeros_like(t)
    for a, f in zip(amps, freqs): 
        x += a * np.sin(2 * np.pi * f * t)

    return x

amps = np.array([9, 10, 2.3])
freqs = np.array([2, 1, 10])
x = getSineSignal(amps, freqs, t)

plt.figure(figsize=(8,6))
plt.plot(t, x, 'r')
plt.xlabel('t')
plt.ylabel('x')
plt.grid(True)

在scipy里的fft函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
fft.fft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None)
'''
x: 输入信号，一维或多维数组（通常为实数或复数）
n: 变换的点数，默认为 x 的长度。如果指定 n, 信号会被截断或零填充到长度 n
axis: 沿哪个轴进行 DFT,默认是 -1(最后一个轴)
norm: 归一化方式：
    None(默认): 不归一化, DFT 输出直接为公式结果。
    "forward": 除以 1(标准 DFT)。
    "backward": 除以 N(逆变换归一化)。
    "ortho": 除以 sqrt(N)（正交归一化）。
overwrite_x: 是否允许修改输入数组以节省内存。
workers: 并行计算的线程数，默认为 None(自动选择)
'''

用之前的画图函数：

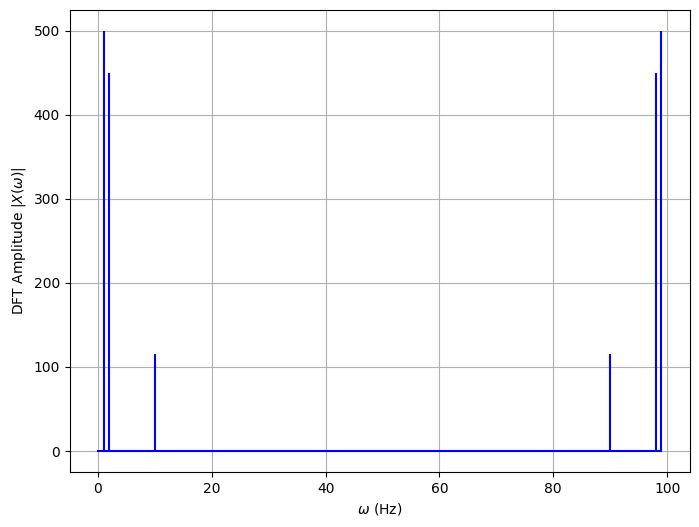
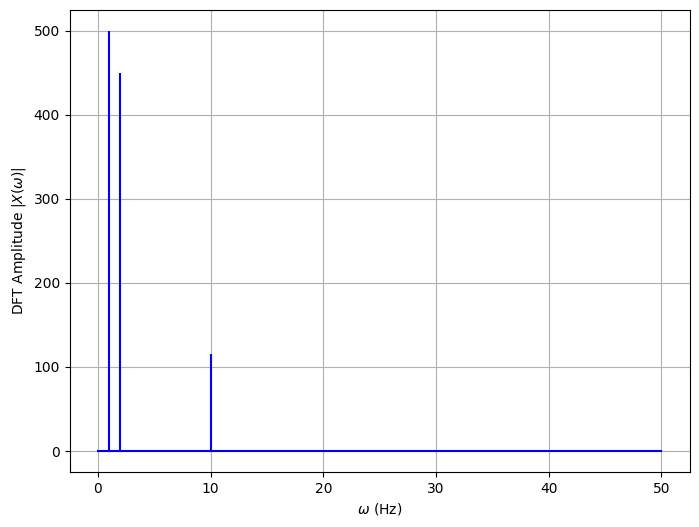
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X_k = fft.fft(x)
N = X_k.size # 信号的采样点数
n = np.arange(N) # 表示频域的索引（对应频率分量的编号）
T = N / rate  # 计算信号的总时长 T（单位：秒）
freq = n / T # 计算频率轴的刻度 freq   n / T 将索引 n 转换为实际频率（Hz）

plt.figure(figsize=(8,6))
plt.stem(freq, abs(X_k), 'b', markerfmt=' ', basefmt='-b') 
# 'b' 表示使用蓝色线条
# markerfmt=' ' 表示茎的顶部不显示标记点
# basefmt='-b' 表示基线为蓝色实线

plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
plt.grid(True)

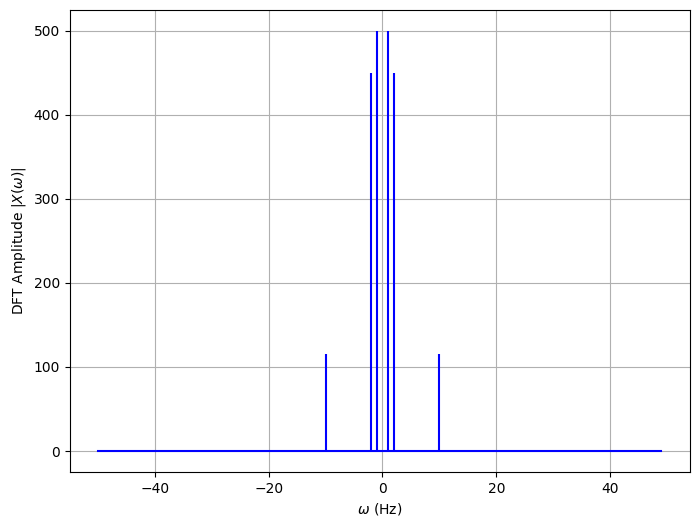
使用fft.fftfreq来画图，会自动画对称的频谱图

1
2
3
4
5
6
freq = fft.fftfreq(N, d=1/rate)  # d 是采样间隔（秒）
plt.figure(figsize=(8,6))
plt.stem(freq, abs(X_k), 'b', markerfmt=' ', basefmt='-b') 
plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
plt.grid(True)

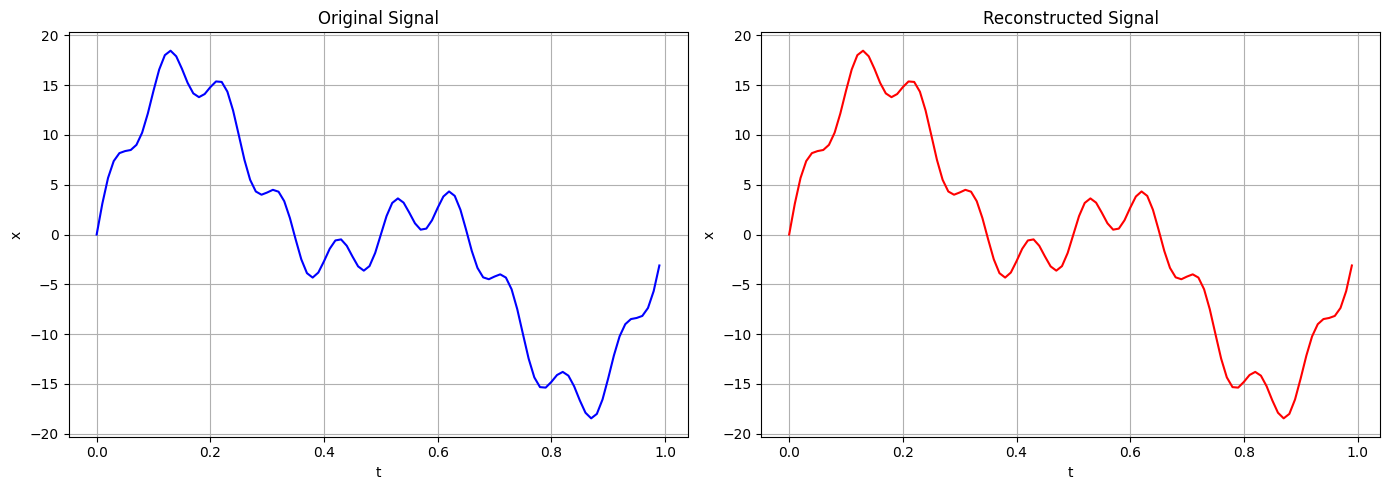
逆变换ifft：

1
2
3
fft.ifft(x, n=None, axis=-1, norm=None, overwrite_x=False, workers=None)
# x: 输入频域信号（复数数组，如 fft.fft 的输出）
# 输出一个复数数组（对于实信号，通常虚部接近 0），表示时域信号。
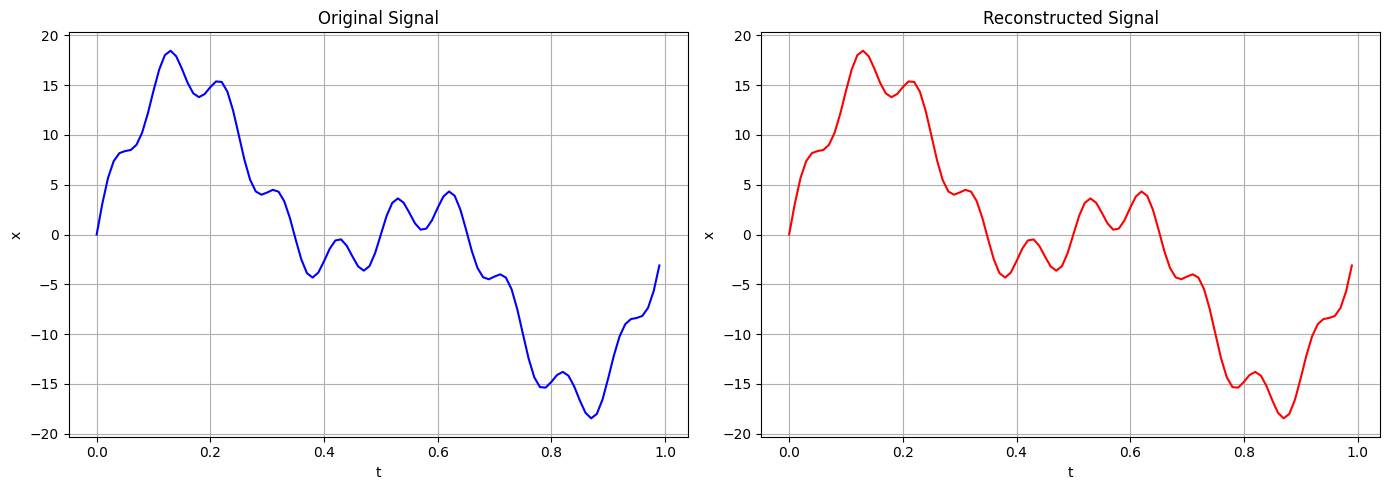
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inv_x = fft.ifft(X_k)

plt.figure(figsize = (14, 5))
plt.subplot(121)
plt.plot(t, x, 'b')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Original Signal')
plt.grid(True)
plt.subplot(122)
plt.plot(t, inv_x, 'r')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Reconstructed Signal')
plt.tight_layout()
plt.grid(True)

rfft是专为实信号设计的 FFT，只计算正频率部分（k = 0 到 N//2），节省内存和计算量。

1
2
3
4
5
6
7
8
X_k_real = fft.rfft(x)
freq_real = fft.rfftfreq(N, d=1/rate)

plt.figure(figsize=(8,6))
plt.stem(freq_real, abs(X_k_real), 'b', markerfmt=' ', basefmt='-b') 
plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
plt.grid(True)

irfft，逆变换，专门用于 rfft 的输出，将正频率部分转换回时域。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
inv_x_real = fft.irfft(X_k_real, n=N)
plt.figure(figsize = (14, 5))
plt.subplot(121)
plt.plot(t, x, 'b')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Original Signal')
plt.grid(True)
plt.subplot(122)
plt.plot(t, inv_x_real, 'r')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Reconstructed Signal')
plt.tight_layout()
plt.grid(True)