SDF，符号距离函数(signed distance function)，是一种表示物体表面与空间中任意点之间距离的函数。

  • 对于物体内部的点，SDF值为正；
  • 对于物体外部的点，SDF值为负；
  • 对于物体表面的点，SDF值为零。
    SDF能够精确描述物体的几何形状和边界，为处理复杂几何问题提供了便利。

比如对于圆形域$\Omega = { \mathbf{x} : x^2 + y^2 < 1 }$，$SDF$函数$\phi(x)$定义为点$x$到边界$\partial \Omega$的最短距离：
$$\phi(x) = 1 - \sqrt{x^2 + y^2}$$

  • $\phi(\mathbf{x}) = 0$，当$\mathbf{x} \in \partial \Omega$；
  • $\phi(\mathbf{x}) > 0$，当$\mathbf{x} \in \Omega$（内部）；
  • $\phi(\mathbf{x}) < 0$，当$\mathbf{x} \notin \Omega$（外部）。

在PINN中，使用SDF为损失函数分配权重，可以防止边界的冲突，比如在边界附近的点物理损失权重非常低，边界损失权重高。

比如下图一个复杂的多边形计算域中，内部点为正（红色），外部点为负（蓝色），数值上为点到多边形边界的最短距离，故外部点越远离边界越蓝，内部点越靠近里面越红，绿色为边界点，此处值为0。

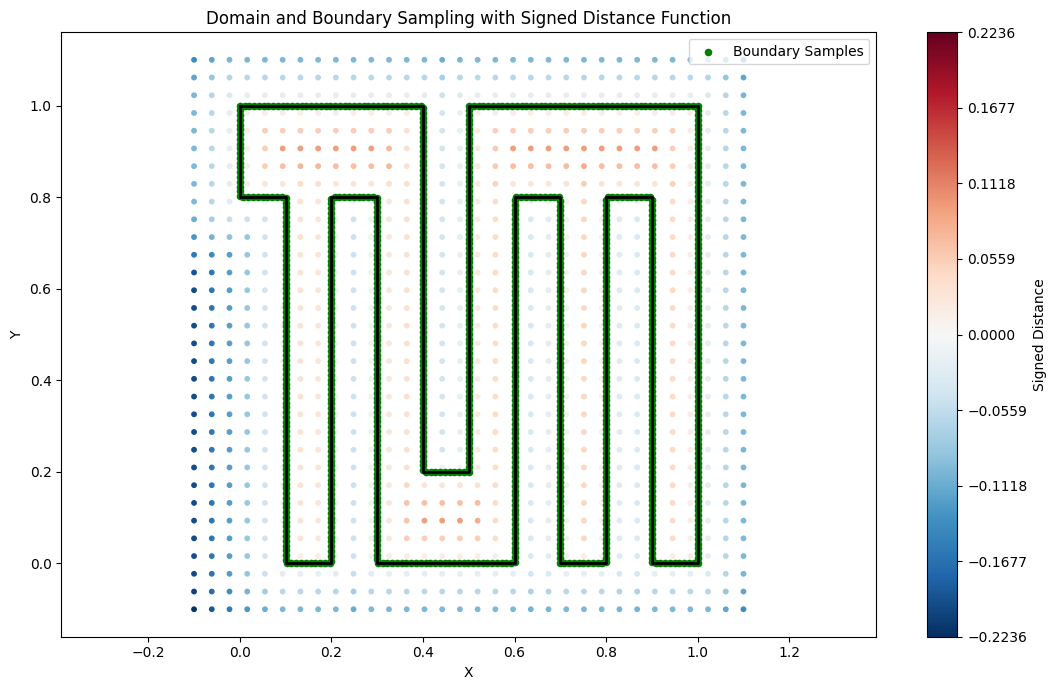
把这些采样点划分为训练集和验证集进行训练，最终得到了对所有点的SDF值预测的模型：

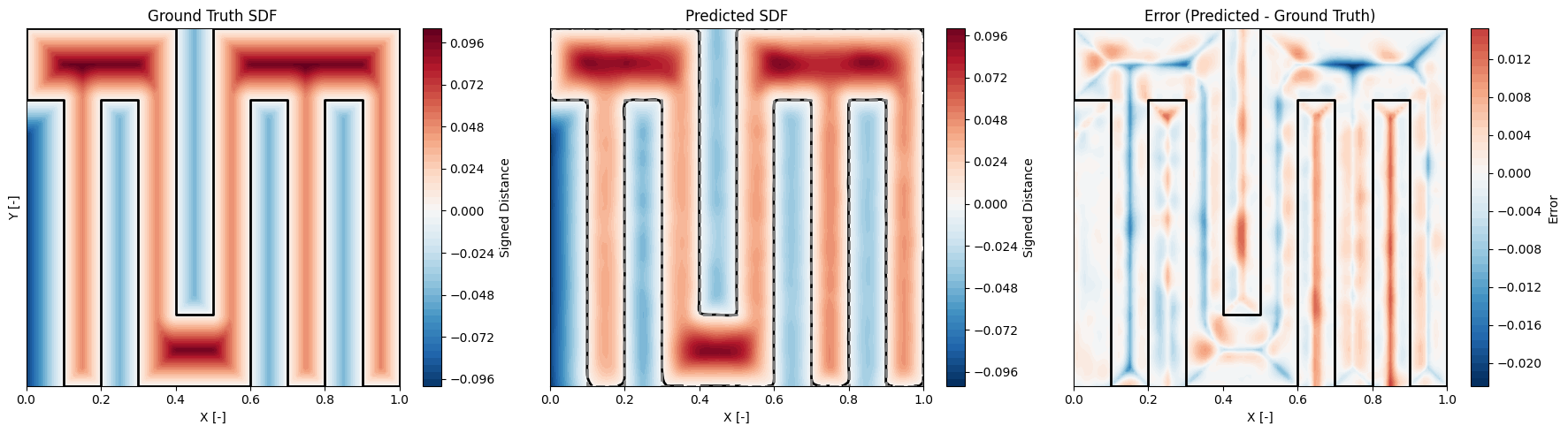
Pytorch版本的具体实现在这里，原作者使用Tensorflow实现了SDF模型的训练，并称预测了该多边形上的Poisson方程，但PINN的预测似乎没有实现，而是在参考场上加了一个随机噪声谎称PINN预测值，后续我也许会实现。

原作者代码中实现了一些有趣实用的算法：多边形内点判定算法，点到多边形的有符号距离，并使用了傅里叶特征嵌入。

参考资料：