3.在Python中实现快速傅里叶变换(FFT)

加快傅里叶变换的解决方案称为Cooley-Tukey算法，该算法依赖于2个关键改进。

Improvement 1 — The Divide-and-Conquer Method

DFT方程是：
$$X[k]=\sum_{n=0}^{N-1}x[n]e^{-i2\pi\frac{k}{N}n}$$
其中$k$的范围从$0$到$N-1$

让我们将其分为2个半部分，偶数索引$n=2m$以及奇数索引$n=2m+1$
$$X_k = \sum_{m=0}^{N/2 - 1} x_{2m} e^{-\frac{2\pi i}{N} (2m) k} + \sum_{m=0}^{N/2 - 1} x_{2m + 1} e^{-\frac{2\pi i}{N} (2m + 1) k}=E_k+e^{-\frac{2\pi i}{N}}O_k$$
其中$k$的范围从$0$到$\frac{N}{2}-1$

因此，将大小为$N$的原始x向量分为$E_k$和$O_k$，每个大小$N/2$。

由于大小为$N$的向量需要$N^2$计算，因此每个减半向量现在都需要$(N^2)/4$计算。这意味着获得原始大小的傅立叶向量只需要$(N^2)/2$计算。

继续这个过程，直到我们得到大小为1的矢量。要注意的是，由于我们将输入数组分为2半，因此$N$必须是2的倍数。如果不是，则可以通过用零填充末端来扩展数组。

由此，时间复杂度从$O(n^2)$变成$O(nlogn)$，其中基底为2。

Improvement 2 — Periodicity of Sinusoidal Functions

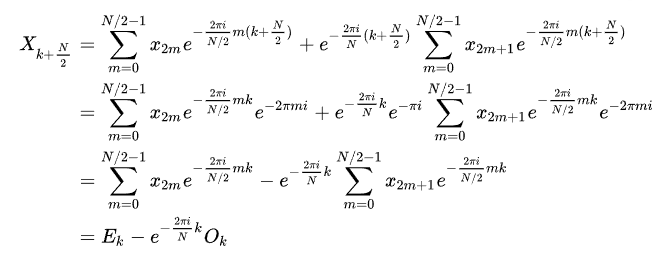
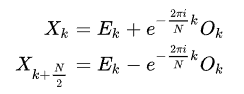
来自https://en.wikipedia.org/wiki/Cooley%E2%80%93Tukey_FFT_algorithm

总而言之，如果$N=2000$，我们只需要计算前1000个值的傅里叶向量，并在下半重复使用。

让我们在Python中实现FFT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def FFT(x):
    N = x.size
    if N == 1:
        return x

    x_even = FFT(x[::2])
    x_odd = FFT(x[1::2])

    k = np.arange(N//2)
    factor = np.exp(-2j * np.pi * k / N)

    arr_1 = x_even + factor * x_odd
    arr_2 = x_even - factor * x_odd

    X_k = np.concatenate([arr_1, arr_2])

    return X_k