在上一篇文章中，我们在Python中实施了离散的傅里叶变换（DFT）。

在本文中，让我们看一下逆过程：将频率值向量转换为时间值的向量。

从数学上讲，反离散的傅里叶变换（IDFT）由以下方式给出：

$$x[n]=\frac{1}{N}\sum_{k=0}^{N-1}X[k]\cdot e^{i2\pi\frac{k}{N}n}$$
其中：

  • $N$是采样数量
  • $n$是当前样本的序号
  • $k$是当前频率
  • $X[k]$是$n$处的DFT
  • $x[n]$是$n$处的iDFT

由于离散傅里叶变换的矩阵是方形且可逆的，因此反向变换是可行的。理想情况下，我们应该能够收回我们的原始嘈杂信号。

前期准备：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
import matplotlib.pyplot as plt

rate = 100 # rate 是采样率（每秒采样点数，单位：Hz）
interval = 1 / rate

t_start = 0
t_end = 1
t = np.arange(t_start, t_end, interval) # (0, 1, 1/100)  时间采样

def getSineSignal(amps, freqs, t):  # 接受振幅和频率数组并生成组合信号的函数
    x = np.zeros_like(t)
    for a, f in zip(amps, freqs): 
        x += a * np.sin(2 * np.pi * f * t)

    return x

amps = np.array([9, 10, 2.3])
freqs = np.array([2, 1, 10])
x = getSineSignal(amps, freqs, t)

def DFT(x):
    N = x.size
    n = np.arange(N)
    k = n.reshape((N, 1))

    e = np.exp(-2j * np.pi * k * n / N)
    X_k = np.dot(e, x)
        
    return X_k

X_k = DFT(x)
N = X_k.size
n = np.arange(N)
T = N / rate
freq = n / T

plt.figure(figsize=(8,6))
plt.stem(freq, abs(X_k), 'b', markerfmt=' ', basefmt='-b')
plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
plt.grid(True)

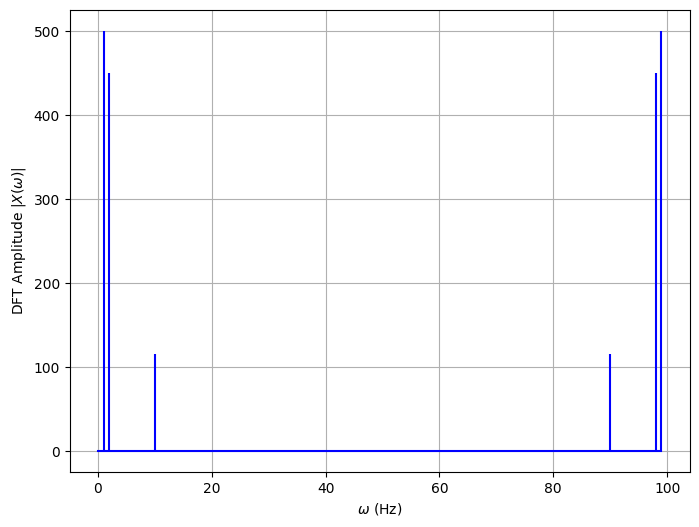
DFT函数返回了一个复数的向量，包含每个频率下的幅度和相位。我们称该向量X_K。

现在，我们将使用X_K收回我们的原始信号。

1
2
3
4
5
6
7
8
9
10
11
12
13
def iDFT(X_k):
    N = X_k.size
    n = np.arange(N)
    k = n.reshape((N,1))

    e = np.exp(2j * np.pi * k * n / N)
    x = np.zeros_like(X_k)
    for row in range(N):
        for col in range(N):
            x[row] += e[row, col] * X_k[col]
    x /= N

    return x.real # 在绘制信号时，我们仅对复数的实数部分感兴趣

补充：取复数的实部和虚部

1
2
3
z1 = 3+4j
print(z1.real) # 3.0
print(z1.imag) # 4.0

重建信号，并将其与原始信号进行比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
inv_x = iDFT(X_k)

plt.figure(figsize = (14, 5))
plt.subplot(121)
plt.plot(t, x, 'b')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Original Signal')
plt.grid(True)
plt.subplot(122)
plt.plot(t, inv_x, 'r')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Reconstructed Signal')
plt.tight_layout()
plt.grid(True)

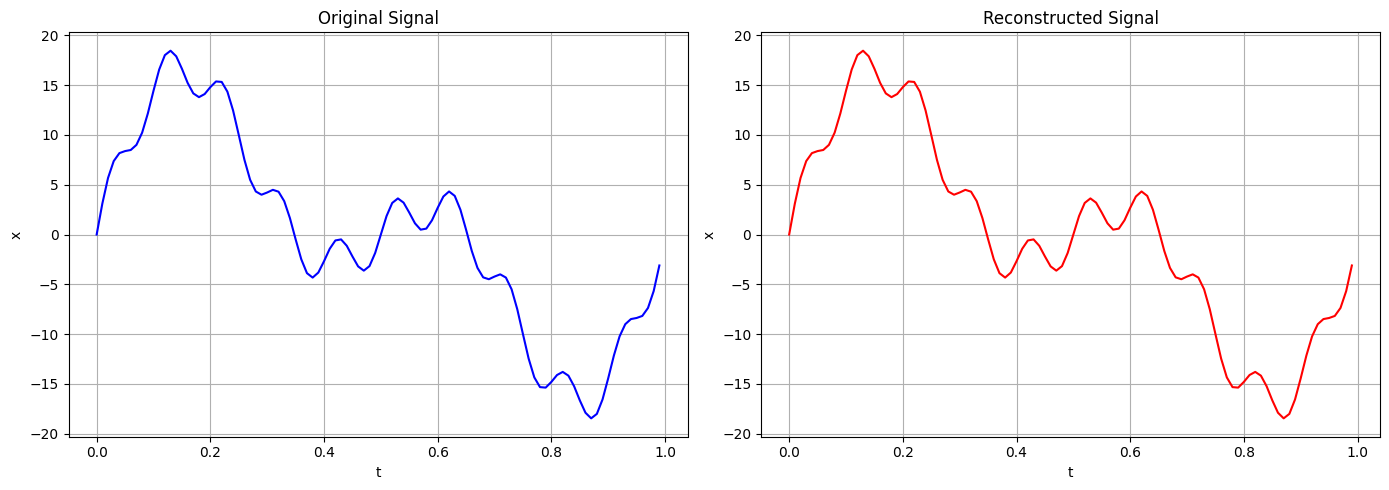
当然，我们有一个干净的信号。这使重建过程变得更加容易

1
2
3
4
5
6
7
8
9
10
plt.figure(figsize = (7, 5))
plt.plot(t, x, 'b', label='Original Signal')
plt.plot(t, inv_x, 'r--', linewidth=2, label='Reconstructed Signal')
plt.xlabel('t')
plt.ylabel('x')
plt.title('Original and Reconstructed Signals')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()

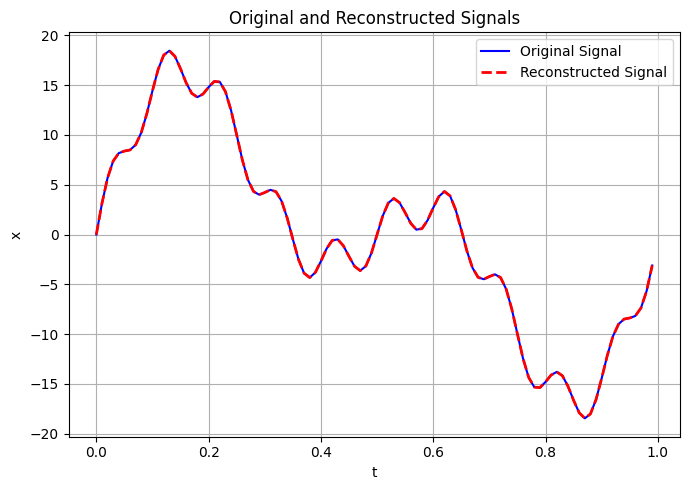
改进：

1
2
3
4
5
6
7
8
9
10
# Loops are slow. So let’s vectorize the iDFT function.
def viDFT(X_k):
    N = X_k.size
    n = np.arange(N)
    k = n.reshape((N,1))

    e = np.exp(2j * np.pi * k * n / N)
    x = np.dot(e, X_k) / N

    return x.real

就像以前一样，矢量化函数的速度快了10倍。