FF-PINN，意思是在输入中添加傅里叶特征(Fourier feature)嵌入，该方法通过使用正弦函数将PINN的输入坐标映射到更高维空间，从而增强了PINN模型的细节表示，从而提高了捕捉精细尺度细节的性能。

具体而言，做了如下变换：
$$
\gamma_{i}(X) = \begin{bmatrix}
\cos(2\pi \beta_{i} X) \
\sin(2\pi \beta_{i} X)
\end{bmatrix}, \quad \text{for } i=1, 2, \ldots, S
$$
这里$\gamma$代表FF，$X$代表PINN的输入向量，参数$\beta$取自高斯分布$N(\mu, \sigma)$。

示意图如下，在输入层与第一层隐藏层之间添加了$FF$层：

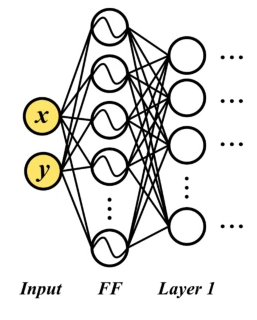
具体代码实现：

1
2
3
4
5
6
7
8
9
10
import torch
import numpy as np

# Fourier feature mapping using PyTorch operations 傅里叶特征映射函数
def input_mapping(x, B): # B: 变换矩阵
    if B is None:
        return x
    else:
        x_proj = torch.matmul(x, B.t()) * (2.0 * np.pi) # B.t() 转置
        return torch.cat([torch.sin(x_proj), torch.cos(x_proj)], dim=-1)

这里我们用$3\times2$的输入向量演示：

1
2
3
x = torch.tensor([[1.0,2.0], [2.0,3.0], [3.0,4.0]])
print(x)
print(x.shape)
1
2
tensor([[1., 2.], [2., 3.], [3., 4.]]) 
torch.Size([3, 2])

生成服从正态分布（高斯分布）的随机数

1
2
3
mapping_size = 10
B = torch.normal(mean=0, std=1.0, size=(mapping_size, 2), dtype=torch.float32)
print(B)
1
2
3
4
5
6
7
8
9
10
tensor([[-1.6859, -1.6255],
        [ 1.1449,  1.1859],
        [ 0.3760, -1.0719],
        [ 1.0152, -0.9373],
        [ 0.8651, -0.2981],
        [-1.1040,  0.6884],
        [ 0.1124, -1.4430],
        [ 0.8184, -0.9454],
        [ 0.6324, -2.4483],
        [-1.2411, -0.4845]])

执行Fourier feature mapping函数中的乘法

1
2
3
4
a = torch.matmul(x, B.t())
a2 = a * (2.0 * np.pi)
print(a2)
print(a2.shape)
1
2
3
4
5
6
7
tensor([[-31.0199,  22.0959, -11.1077,  -5.4000,   1.6900,   1.7143, -17.4269,
          -6.7378, -26.7930, -13.8870],
        [-51.8264,  36.7408, -15.4802,  -4.9107,   5.2529,  -0.8968, -25.7872,
          -7.5357, -38.2028, -24.7295],
        [-72.6329,  51.3856, -19.8528,  -4.4214,   8.8158,  -3.5079, -34.1476,
          -8.3336, -49.6126, -35.5720]])
torch.Size([3, 10])

返回的$sin$操作，$cos$同理：

1
2
print(torch.sin(a2))
print(torch.sin(a2).shape)
1
2
3
4
5
6
7
tensor([[ 0.3857, -0.1046,  0.9937,  0.7728,  0.9929,  0.9897,  0.9890, -0.4391,
         -0.9960, -0.9689],
        [-1.0000, -0.8182, -0.2258,  0.9804, -0.8574, -0.7813, -0.6088, -0.9498,
         -0.4827,  0.3924],
        [ 0.3674,  0.9002, -0.8432,  0.9580,  0.5720,  0.3582, -0.3986, -0.8872,
          0.6075,  0.8492]])
torch.Size([3, 10])

按最后一个维度进行拼接：

1
2
3
a3 = torch.cat([torch.sin(a2), torch.cos(a2)], dim=-1)
print(a3)
print(a3.shape)
1
2
3
4
5
6
7
8
9
10
tensor([[ 0.3857, -0.1046,  0.9937,  0.7728,  0.9929,  0.9897,  0.9890, -0.4391,
         -0.9960, -0.9689,  0.9226, -0.9945,  0.1119,  0.6347, -0.1190, -0.1430,
          0.1476,  0.8984, -0.0894,  0.2476],
        [-1.0000, -0.8182, -0.2258,  0.9804, -0.8574, -0.7813, -0.6088, -0.9498,
         -0.4827,  0.3924,  0.0099,  0.5749, -0.9742,  0.1970,  0.5146,  0.6241,
          0.7934,  0.3129,  0.8758,  0.9198],
        [ 0.3674,  0.9002, -0.8432,  0.9580,  0.5720,  0.3582, -0.3986, -0.8872,
          0.6075,  0.8492, -0.9300,  0.4356,  0.5376, -0.2869, -0.8203, -0.9337,
         -0.9171, -0.4615,  0.7943, -0.5280]])
torch.Size([3, 20])

这里通过傅里叶特征映射，把torch.Size([3, 2]) 变成了  torch.Size([3, 20]) 。注意mapping_size = 10，因为包含正弦和余弦两个部分，所以输出是 2 * mapping_size 。

具体在PINN中的使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Fourier feature mapping using PyTorch operations 
def input_mapping(x, B): # B: 变换矩阵
    if B is None:
        return x
    else:
        x_proj = torch.matmul(x, B.t()) * (2.0 * np.pi) # B.t() 转置
        return torch.cat([torch.sin(x_proj), torch.cos(x_proj)], dim=-1)

# Custom layer for Fourier features
class FourierFeatures(nn.Module):
    def __init__(self, B=None):
        super(FourierFeatures, self).__init__()
        self.B = B  # B is a tensor or None

    def forward(self, inputs):
        return input_mapping(inputs, self.B)
    
# Create B_dict with different Fourier feature mappings 不同类型的映射矩阵
mapping_size = 256
B_dict = {
    'none': None,
    'gauss_1': torch.normal(mean=0, std=1.0, size=(mapping_size, 2), dtype=torch.float32),
    'gauss_10': torch.normal(mean=0, std=10.0, size=(mapping_size, 2), dtype=torch.float32),
    'gauss_100': torch.normal(mean=0, std=100.0, size=(mapping_size, 2), dtype=torch.float32),
}

B = B_dict['gauss_1']

把FourierFeatures类嵌入神经网络，这里是一个符号距离函数（SDF）网络：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Define the MLP model with Fourier features
class NeuralSDF(nn.Module):
    def __init__(self, B=None):
        super(NeuralSDF, self).__init__()
        layers = []
        # Input layer: Fourier features
        self.fourier = FourierFeatures(B=B)

        # 6 hidden layers with 512 units and ReLU activation
        layers.append(nn.Linear(2*mapping_size, 512))
        layers.append(nn.ReLU())
        for _ in range(5):
            layers.append(nn.Linear(512, 512))
            layers.append(nn.ReLU())
        # Additional dense layers
        layers.append(nn.Linear(512, 32))
        layers.append(nn.Linear(32, 1))  # Output layer 输出 SDF 值
        self.mlp = nn.Sequential(*layers)

    def forward(self, x):
        x = self.fourier(x) # 输入经过 FourierFeatures 层映射到高维特征
        return self.mlp(x)

实例化模型：

1
neural_SDF = NeuralSDF(B=B)

参考资料：