在处理录制视频时，发现有背景噪音，如何从音频中去除？

需要识别噪声的频率，然后过滤出来。

如何确定频率？答案是傅里叶频率。

把信号分解为正弦波和余弦波，然后可以识别每个wave的幅度(amplitude)，频率(frequency)和相位(phase)，绘制每个频率的图像，我们可以隔离对信号贡献度最大的幅度。

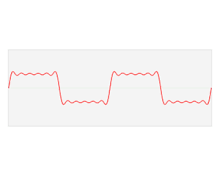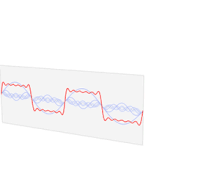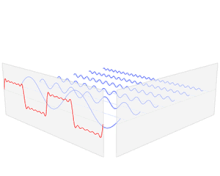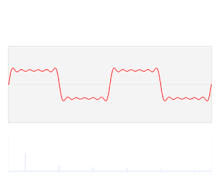
在连续函数上的傅里叶变换：

但在现实中，信号是离散的，因此我们有离散的傅里叶变换(DFT)：

在这里：

  • $N$是采样数量
  • $n$是当前样本的序号
  • $k$是当前频率
  • $x[n]$是$n$处信号值
  • $X[k]$是当前$k$对应的DFT

接下来让我们在Python中见证DFT的魔力。

首先导入一些库

1
2
import numpy as np
import matplotlib.pyplot as plt

接下来，定义采样速率以定义时间的数组

1
2
3
4
5
6
7
rate = 100 # rate 是采样率（每秒采样点数，单位：Hz）
interval = 1 / rate

t_start = 0
t_end = 1
t = np.arange(t_start, t_end, interval) # (0, 1, 1/100)  时间采样
print(len(t)) # 100

现在，我们要生成一个由3个正弦波组合的信号。让我们编写一个接受振幅和频率数组并生成组合信号的函数。

1
2
3
4
5
6
def getSineSignal(amps, freqs, t):  # 接受振幅和频率数组并生成组合信号的函数
    x = np.zeros_like(t)
    for a, f in zip(amps, freqs): 
        x += a * np.sin(2 * np.pi * f * t)

    return x

添加3个正弦波，幅度依次是9，10，2.3，频率依次是2，1，10

1
2
3
amps = np.array([9, 10, 2.3])
freqs = np.array([2, 1, 10])
x = getSineSignal(amps, freqs, t)

这三个正弦波的图像如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
signal1 = amps[0] * np.sin(2 * np.pi * freqs[0] * t)
signal2 = amps[1] * np.sin(2 * np.pi * freqs[1] * t)
signal3 = amps[2] * np.sin(2 * np.pi * freqs[2] * t)

fig, axs = plt.subplots(1, 3, figsize=(12, 3))  # 1行3列

axs[0].plot(t, signal1, 'r')
axs[0].set_xlabel('t')
axs[0].set_ylabel('x')
axs[0].grid()

axs[1].plot(t, signal2, 'r')
axs[1].set_xlabel('t')
axs[1].set_ylabel('x')
axs[1].grid()

axs[2].plot(t, signal3, 'r')
axs[2].set_xlabel('t')
axs[2].set_ylabel('x')
axs[2].grid()

plt.tight_layout()  # 自动调整子图间距
plt.show()

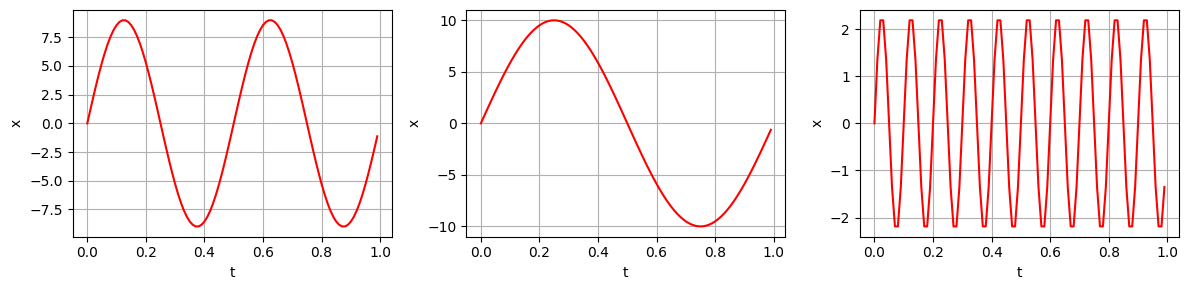
组合后的信号：

1
2
3
4
5
plt.figure(figsize=(8,6))
plt.plot(t, x, 'r')
plt.xlabel('t')
plt.ylabel('x')
plt.grid(True)

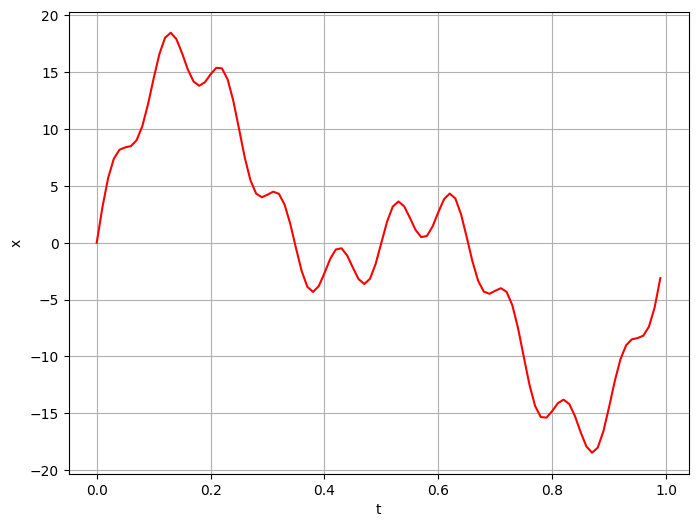
现在，让我们编写一个在数组上执行DFT操作的函数。

1
2
3
4
5
6
7
8
9
10
11
def DFT(x):
    N = x.size
    n = np.arange(N)
    k = n.reshape((N, 1)) # 频率索引  0到N-1，N个采样点，最多可能由N个频率下的曲线合成， 包含pi的频率已经隐含在公式中了

    e = np.exp(-2j * np.pi * k * n / N)  #  这个矩阵是 DFT 的基函数矩阵，包含了所有频率分量的复指数。 矩阵的每一行对应一个频率
    X_k = np.zeros_like(k, dtype=np.complex128)  # 包含了复数，要声明这是个复杂的数组
    for row in n: # 对应频域索引 k 
        for col in n:  # 对应时间域索引 n
            X_k[row] += e[row, col] * x[col]
    return X_k  # 一个 N×1 的复数数组，表示输入信号在频域的表示

补充一下numpy中的exp算法：

1
2
3
4
5
a = np.array([[1,1,2],[1,2,1]])
test = np.exp(a)  # 对矩阵内所有元素e^
print(test)

# [[2.71828183 2.71828183 7.3890561 ] [2.71828183 7.3890561 2.71828183]]

让我们来验证一下：

1
2
3
4
5
6
7
print(x.shape)
print(x[:5])

'''
(100,)
[0.         3.10781038 5.67897131 7.37436411 8.17458802]
'''

1
2
3
4
5
6
7
8
9
10
11
12
X_k = DFT(x)
print(X_k.shape)
print(X_k[:5])

'''
(100, 1)
[[-4.35207426e-14+0.00000000e+00j]
 [ 7.10542736e-14-5.00000000e+02j]
 [-4.44089210e-16-4.50000000e+02j]
 [-1.62536651e-13-7.62723218e-14j]
 [-4.39648318e-14+1.25455202e-14j]]
'''

让我们绘制振幅随频率变化的图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
X_k = DFT(x)
N = X_k.size # 信号的采样点数
n = np.arange(N) # 表示频域的索引（对应频率分量的编号）
T = N / rate  # 计算信号的总时长 T（单位：秒）
freq = n / T # 计算频率轴的刻度 freq   n / T 将索引 n 转换为实际频率（Hz）

plt.figure(figsize=(8,6))
plt.stem(freq, abs(X_k), 'b', markerfmt=' ', basefmt='-b') 
# 'b' 表示使用蓝色线条
# markerfmt=' ' 表示茎的顶部不显示标记点
# basefmt='-b' 表示基线为蓝色实线

plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
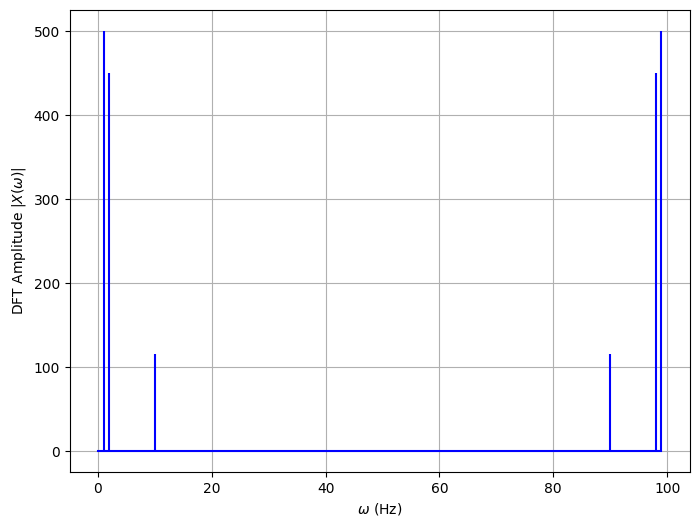
plt.grid(True)

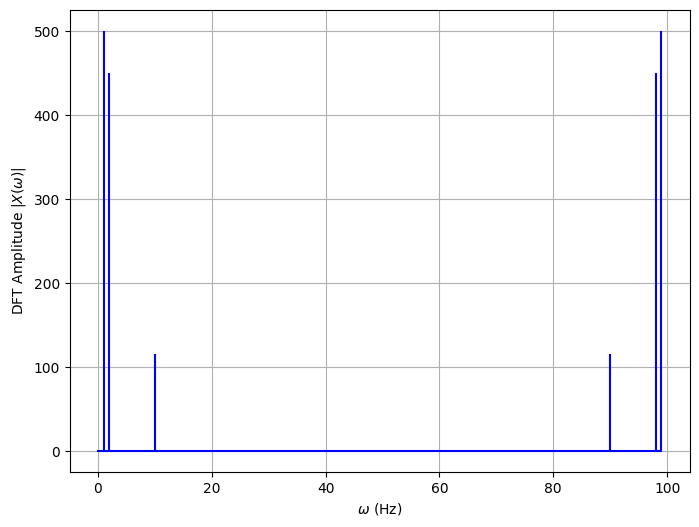
该图称为振幅频谱图，在采样率的一半上是对称的。这是一个被称为Nyquist-Shannon定理的结果。

注意abs绝对值可以计算复数的模，也就是幅度：

1
2
z1 = 3 + 4j
print(abs(z1))  # 5.0

我们可以看到3个主要信号的频率！直接把振幅打印出来：

1
2
3
4
5
6
7
8
9
print(abs(X_k)[1])
print(abs(X_k)[2])
print(abs(X_k)[10])

'''
[500.]
[450.]
[115.]
'''

让我们卸下右半，然后放大频谱。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n_oneside = N // 2
# 对于实数输入信号，DFT 的频谱是对称的（负频率和正频率幅度相同），因此通常只分析 0 到 Nyquist 频率（采样率的一半）之间的部分
f_oneside = freq[:n_oneside] # 提取单边频率轴
X_k_oneside = X_k[:n_oneside] / n_oneside # 计算单边幅度谱并进行归一化 频率 1，2，10对应的幅度是10，9，2.3
# 归一化是为了让单边幅度谱的幅度值反映信号的真实强度，通常在实信号的单边谱中需要将幅度除以 N/2

plt.figure(figsize = (12, 6))
plt.subplot(121)
plt.stem(f_oneside, abs(X_k_oneside), 'b', markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.ylabel('DFT Amplitude |X(freq)|')
plt.grid(True)
plt.subplot(122)
plt.stem(f_oneside, abs(X_k_oneside), 'b', markerfmt=" ", basefmt="-b")
plt.xlabel('Freq (Hz)')
plt.xlim(0, 12) # 限制 x 轴范围为 0 到 12 Hz，放大低频区域以观察细节
plt.tight_layout()
plt.grid(True)

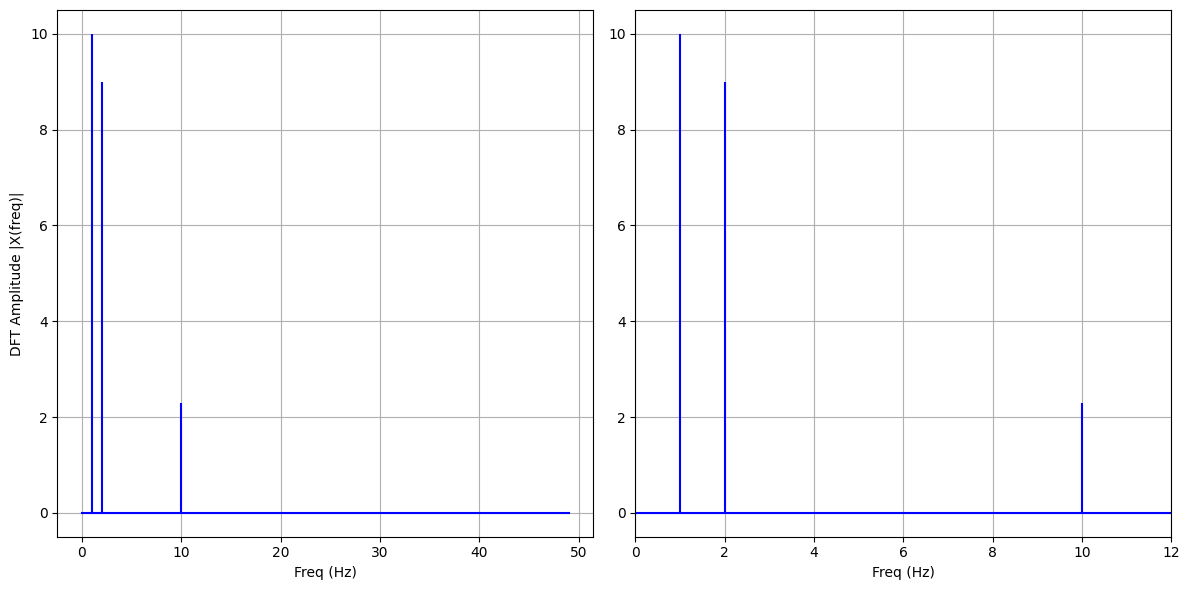
可以看到，频率和振幅与我们最初的正弦波相匹配。

使用numpy矩阵点乘改进我们的DFT算法：

1
2
3
4
5
6
7
8
9
def vDFT(x):
    N = x.size
    n = np.arange(N)
    k = n.reshape((N, 1))

    e = np.exp(-2j * np.pi * k * n / N)
    X_k = np.dot(e, x)
        
    return X_k

1
2
3
4
5
6
7
8
9
10
11
X_k = vDFT(x)
N = X_k.size
n = np.arange(N)
T = N / rate
freq = n / T

plt.figure(figsize=(8,6))
plt.stem(freq, abs(X_k), 'b', markerfmt=' ', basefmt='-b')
plt.xlabel(r'$\omega$ '+'(Hz)')
plt.ylabel('DFT Amplitude '+r'$|X(\omega)|$')
plt.grid(True)

效果是一样的，速度上快了大约10倍。