Dual-Balancing PINN论文阅读（上）

Physics-Informed Neural Networks

核心是构建一个带参数 $\theta$ 的神经网络来学习PDE的近似解 $\hat{u}_\theta (\mathbf{x}, t)$

$\begin{align*} \mathcal{N}_{\mathbf{x}, t}[u(\mathbf{x}, t)] &= f(\mathbf{x}, t), \quad \mathbf{x} \in \Omega, \, t \in [0, T] \\ \mathcal{B}_{\mathbf{x}, t}[u(\mathbf{x}, t)] &= g(\mathbf{x}, t), \quad \mathbf{x} \in \partial\Omega, \, t \in [0, T] \\ u(\mathbf{x}, 0) &= h(\mathbf{x}), \quad \mathbf{x} \in \Omega \end{align*}$

在时空域$(\Omega \times [0, T])$中采样点$\left{ \left( \mathbf{X}i^r, t_i^r \right) \right}{i=1}^{N_r}$，计算PDE残差损失：

$\mathcal{L}^r(\theta) = \frac{1}{N_r} \sum_{i=1}^{N_r} \left\| \mathcal{N}_{\mathbf{x}, t} \left[ \hat{u}_\theta \left( \mathbf{x}_i^r, t_i^r \right) \right] - f \left( \mathbf{x}_i^r, t_i^r \right) \right\|^2$

再加上一众条件损失，如边界条件，初始条件，以及额外的数据。

在PINN的训练中，权重系数是一个影响巨大却难以调节的数字，许多学者寻找动态权重的方法，当前主要的两种路线是the learning approach and the calculating approach。

learning approach视权重系数为可学习的参数，在网络中一同优化；calculating approach以neural tangent kernel (NTK)的视角，基于梯度幅值的比率$\left| \nabla\theta \mathcal{L}^r \right| / \left| \nabla\theta \mathcal{L}^i \right|$对权重进行计算。DB-PINN就是对现有calculating approach中的具体做法GW-PINN进行补充。

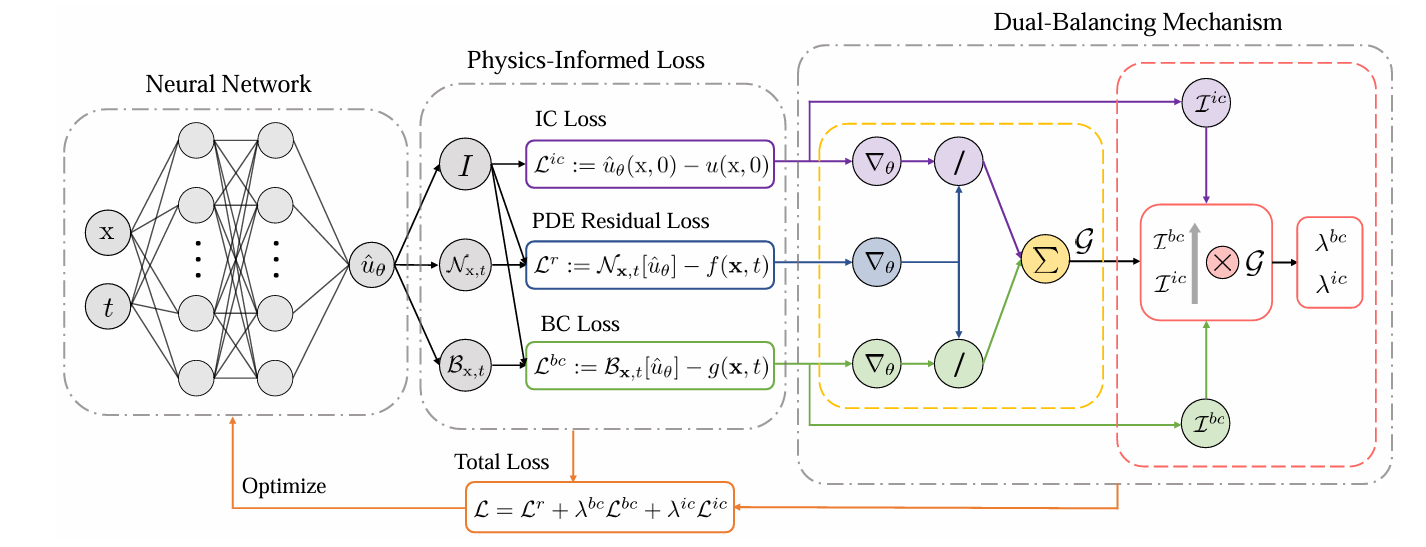
GW-PINN

旨在跨平衡(inter-balancing)，如上图中黄色边框内部所示。以往研究表明，PDE残差通常在各损失项中占主导地位，现在把残差项的权重系数固定为1，在训练过程中调整其余条件损失项的权重。

$\mathcal{G} = \sum_{i=1}^{M} \frac{\max\left\{ \left| \nabla_\theta \mathcal{L}^r \right| \right\}}{\left| \nabla_\theta \lambda^i \mathcal{L}^i \right|}$

通常总损失包括四个原子损失，残差损失$Lr$，边界损失$L{bc}$，初始损失$L{ic}$，数据损失$L{d}$，

$\mathcal{L} = L_r + \lambda_{bc} L_{bc} + \lambda_{ic} L_{ic} + \lambda_d L_d$

实际训练时常出现梯度失衡：某一项对网络参数的反传梯度远大于其它项，导致别的项“学不到东西”。

GW-PINN要做的，就是让各类损失对网络参数的梯度量级对齐。做法是：给每个条件项一个权重

$\lambda_i \propto \frac{s_r}{s_i}$

其中 $s_r$ 是“残差项的梯度尺度”，$s_i$ 是第 $i$ 个条件项（$bc,ic,d$）的梯度尺度。这样当某条件项梯度偏小，它的 $\lambda_i$ 就被放大，反之缩小，实现跨类（inter）的对齐。

基于不同的 $s_r$ 和 $s_i$ 算法，GW-PINN有3种不同实现：

method 1，mean 版：

$s_r = \max\left| \nabla_\theta L_r \right|, \quad s_i = \operatorname{mean}\left| \nabla_\theta L_i \right|$

更新权重：

$\lambda_i \leftarrow (1 - \alpha)\lambda_i + \alpha \cdot \frac{s_r}{s_i}$

这里用了EMA(Exponential Moving Average)平滑进行权重更新，抑制瞬时噪声，比如$\alpha$ 取0.1

method 2，std 版：

$s_r = std\left( \nabla_\theta L_r \right), \quad s_i = std\left( \nabla_\theta L_i \right)$

同上更新

method 3，kurt 版：

先构造$\text{cov} = \text{std}/\text{kurt}$，再更新权重：

$\lambda_i \leftarrow (1 - \alpha)\lambda_i + \alpha \cdot \frac{\text{cov}_r}{\text{cov}_i}$

在代码中，以 method 1 为例：

if method == 1:
	# max/avg
	lamb_hat = maxr/meanb
	lambd_bc     = (1-alpha_ann)*lambd_bc + alpha_ann*lamb_hat 
	lamb_hat = maxr/meani
	lambd_ic     = (1-alpha_ann)*lambd_ic + alpha_ann*lamb_hat 
	lamb_hat = maxr/meand
	lambd_d      = (1-alpha_ann)*lambd_d + alpha_ann*lamb_hat

要用到的 max mean std kurt 由 loss_grad_stats 和 loss_grad_max_mean 函数给出：

stdr,kurtr=loss_grad_stats(l_reg, net)   
stdb,kurtb=loss_grad_stats(l_bc, net)
stdi,kurti=loss_grad_stats(l_ic, net)
stdd,kurtd=loss_grad_stats(l_data, net)

maxr,meanr=loss_grad_max_mean(l_reg, net)  
maxb,meanb=loss_grad_max_mean(l_bc, net,lambg=lambd_bc)  
maxi,meani=loss_grad_max_mean(l_ic, net,lambg=lambd_ic)
maxd,meand=loss_grad_max_mean(l_data, net,lambg=lambd_d)

注意为了稳定，每 10 个 Adam step 更新一次权重（LBFGS更新太慢，一般不在这里更新了）

1	if epoch % mm == 0: # mm = 10

最后得到的权重带入总损失计算：

1	loss = l_reg + lambd_bc.item()l_bc + lambd_ic.item()l_ic + lambd_d.item()*l_data

注意.item() 明确切到 Python 标量，不参与计算图（不希望 λ 反传）

max mean std kurt 的算法

以 method 1 为例，残差项的“尺度”为

$S_r = \max_{\theta} \left| \nabla_{\theta} L_r \right|$

也就是：把 $L_r$ 对“所有可训练参数 $\theta$ ”的梯度，取绝对值后的全局最大值。

条件项（bc/ic/data）的“尺度”为

$S_i = \operatorname{mean}_{\theta} \left| \nabla_\theta (\lambda_i L_i) \right|$

也就是：对每个条件项 $L_i$，在当前权重 $\lambda_i$ 下，对所有参数的梯度，取绝对值后的整体均值。注意这里有$\lambda_i$，对应着 loss_grad_max_mean 函数中的 lambg 参数，因为残差项 $L_r$ 权重默认为1，故无需传入 lambg 参数。

loss_grad_max_mean 函数的具体实现如下

def loss_grad_max_mean(loss, net, lambg=1):
    """
    inputs: loss: loss function ; net: the NN model; lambg : term for weighted stats (optional)
    outputs: max and mean
    """
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    grad_ = torch.zeros((0), dtype=torch.float64,device=device)
    
    # 遍历网络所有层，只看 nn.Linear 的参数（权重和偏置）
    for m in net.modules():
        if not isinstance(m, nn.Linear): 
            continue

        if(m == 0):
            w = torch.abs(lambg*grad(loss, m.weight, retain_graph=True, allow_unused=True)[0])
            b = torch.abs(lambg*grad(loss, m.bias, retain_graph=True, allow_unused=True)[0])        
            grad_ = torch.cat((w.view(-1), b))


        else:
            w = torch.abs(lambg*grad(loss, m.weight, retain_graph=True, allow_unused=True)[0]) # 绝对值
            
            if grad(loss, m.bias, retain_graph=True, allow_unused=True)[0] is None:
                b = None
            else:
                b = torch.abs(lambg*grad(loss, m.bias, retain_graph=True, allow_unused=True)[0])    
            
            if b is not None:
                grad_ = torch.cat((grad_,w.view(-1), b))
            else:
                grad_ = torch.cat((grad_,w.view(-1)))
    
    # 梯度绝对值的最大与平均
    maxgrad = torch.max(grad_)
    meangrad = torch.mean(grad_)
    
    return maxgrad,meangrad