Dual-Balancing PINN论文阅读（下）

DB-PINN

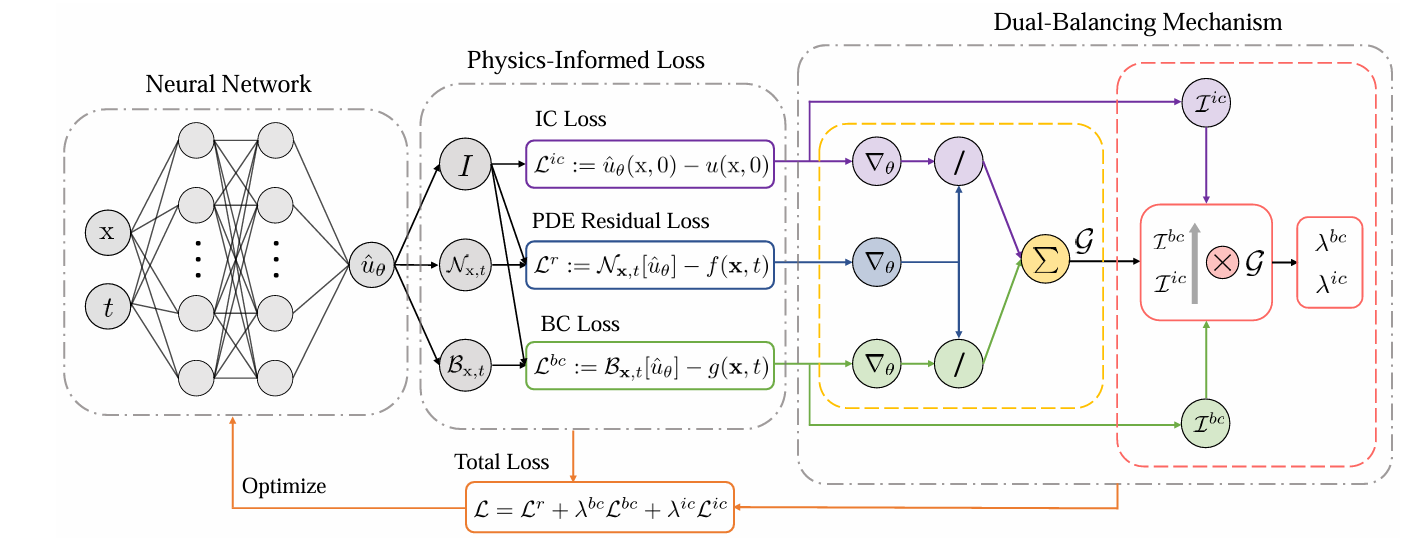
现在我们看到上图中红色框内部分，结合了难度系数后，GW-PINN过渡到了DB-PINN，融合了跨平衡(inter-balancing)和内平衡(intra-balancing)。

类似GW-PINN中method 1用max和mean，以DB-PINN中的DB_PINN_mean为例，首先等价做GW-PINN，对每个条件项$i \in { \text{bc}, \text{ic}, \text{d} }$计算比值：
$$
\frac{S_r}{S_i} = \frac{\max |\nabla L_r|}{\operatorname{mean} |\lambda_i \nabla L_i|}
$$
然后求和$\sum \frac{S_r}{S_i}=G$，得到总尺度，命名为 hat_all 。

1	hat_all = maxr/meanb + maxr/meani + maxr/meand

直觉：如果条件项整体比 PDE 残差“弱”很多，hat_all 就会大，后面三项条件的总权重会被整体抬升，先把大盘尺度对齐。

现在开始把总尺度分配给内部。

首先介绍下历史平均：给定一串向量$x_1, x_2, \ldots, x_t$，每当新来一个 $x_t$ 时，更新“到目前为止的算术平均”：
$$\mu_t = \frac{1}{t} \sum_{k=1}^{t} x_k$$
直接照定义重算要把全部历史都存起来。在线做法的等价递推是：
$$\mu_t = \mu_{t-1} + \frac{1}{t}(x_t - \mu_{t-1})=\left(1 - \frac{1}{t}\right)\mu_{t-1} + \frac{1}{t} x_t$$

现在我们设立难度指数 $I$ ， $k$ 是第 $k$ 次权重更新（每 mm 步更新一次）：
$$I^{(k)} = \frac{L^{(k)}}{\mu^{(k)}}$$
注意这里是逐元素/分量除法，其中：
$$L^{(k)} = \left[ L_r^{(k)}, L_{bc}^{(k)}, L_{ic}^{(k)}, L_d^{(k)} \right]$$
这是当前第 $k$ 次权重更新的4个原子损失
$$\mu^{(k)} = \left[ \mu_r^{(k)}, \mu_{bc}^{(k)}, \mu_{ic}^{(k)}, \mu_d^{(k)} \right]$$
这是到第 $k$ 次权重更新为止的历史均值，是$L^{(k)}$的均值，参考$\mu_t$的式子，有
$$\mu^{(k)} = \left(1 - \frac{1}{k}\right)\mu^{(k-1)} + \frac{1}{k} L^{(k)}$$
注意这是对每个原子损失项来说的，每次权重更新都会进入一个新的$L^{(k)}$，与之前的$L^{(k)}$共同计算均值。在代码中，历史均值为running_mean_L；k为N_l，初始为0，每次更新+1；L_t = torch.stack((l_reg, l_bc, l_ic, l_data))，即当前的$L^{(k)}$，难度指数l_t_vector = L_t/running_mean_L，这正对应了$I^{(k)} = \frac{L^{(k)}}{\mu^{(k)}}$。

1
2
3

mean_param = (1. - 1 / N_l) 
running_mean_L = mean_param * running_mean_L + (1 - mean_param) * L_t.detach()
l_t_vector = L_t/running_mean_L

这时要把总尺度 $G$ ，也就是hat_all分配给3个条件项，按照难度系数看：
$$I = \left[ \frac{L_{r}}{\mu_{r}}, \frac{L_{bc}}{\mu_{bc}}, \frac{L_{ic}}{\mu_{ic}}, \frac{L_d}{\mu_d} \right]$$
谁的当前损失相对其历史均值更大，$I$ 更大，也就代表更难训练。注意l_t_vector[0]是$\frac{L_{r}}{\mu_{r}}$，残差不参与 $G$ 的分配，所以：

1
2
3

hat_bc = hat_all* l_t_vector[1]/torch.sum(l_t_vector[1:])  
hat_ic = hat_all* l_t_vector[2]/torch.sum(l_t_vector[1:])  
hat_d = hat_all* l_t_vector[3]/torch.sum(l_t_vector[1:])

$$
\hat{\lambda}{bc} = G \cdot \frac{I{bc}}{I_{bc} + I_{ic} + I_d}, \quad \hat{\lambda}{ic} = G \cdot \frac{I{ic}}{I_{bc} + I_{ic} + I_d}, \quad \hat{\lambda}d = G \cdot \frac{I_d}{I{bc} + I_{ic} + I_d}.
$$

这些$\hat{\lambda}_{bc}$等，相当于即时建议权重。

最终进行无超参、稳健的在线平滑更新权重系数：
$$\lambda_i \leftarrow \left(1 - \frac{1}{N_l}\right)\lambda_i + \frac{1}{N_l} \hat{\lambda}_i$$
随着权重更新次数的增多，$\frac{1}{N_l}$ 越后期越小，越平稳。类比GW-PINN中的EMA更新：
$$
\lambda_i \leftarrow (1 - \alpha)\lambda_i + \alpha \cdot \frac{s_r}{s_i}
$$
$\frac{1}{N_l}$ 代替了 $\alpha$ ，$\hat{\lambda}_i$ 代替了 $\frac{s_r}{s_i}$ 。

lambd_bc = lam_avg_bc + 1/N_l*(hat_bc - lam_avg_bc)  
lambd_ic = lam_avg_ic + 1/N_l*(hat_ic - lam_avg_ic)
lambd_d =  lam_avg_d  + 1/N_l*(hat_d - lam_avg_d)

# 储存上次的lambd
lam_avg_bc = lambd_bc
lam_avg_ic = lambd_ic
lam_avg_d = lambd_d

注意首次开始训练时会把以下值初始化为0，使得第一次更新权重时的历史均值就是当前损失。

if epoch == 0:
	lam_avg_bc = torch.zeros(1, device=device)
	lam_avg_ic = torch.zeros(1, device=device)
	lam_avg_d = torch.zeros(1, device=device)
	running_mean_L = torch.zeros(1, device=device)

DB_PINN_std方法，DB_PINN_kurt方法类似，只是更改了hat_all的算法。