Jacobian Matrix

考虑$f(x)=x^2$，求导得$\frac{df}{dx}=2x$

当进入多元函数(Multi-Variable Functions)，比如$f(x_1, x_2)=x_1^2+3x_1 x_2 +x_2^2$，则：
$$
\frac{\partial f}{\partial x_1} = 2x_1 + 3x_2 \quad \frac{\partial f}{\partial x_2} = 3x_1 + 2x_2
$$
当我们不仅有一个包含多个变量的函数，而且有多个函数，且均为多元函数：
$$
\mathbf{f}(\mathbf{x}) = \begin{pmatrix} f_1(x_1, x_2) \ f_2(x_1, x_2) \end{pmatrix} = \begin{pmatrix} x_1^2 + x_2 \ x_1 + x_2^2 \end{pmatrix}
$$
上式代表二维输入空间到二维输出空间的映射

现在我们定义雅可比矩阵(Jacobian Matrix)：
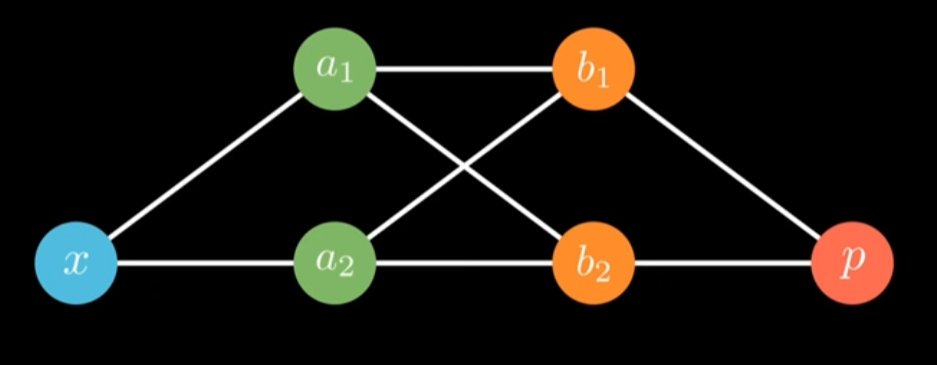
$$
J_f = \begin{pmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} \ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} \end{pmatrix} = \begin{pmatrix} 2x_1 & 1 \ 1 & 2x_2 \end{pmatrix}
$$

Application: Neural Networks

上面是一个$[1, 2, 2, 1]$的全连接神经网络，我们有以下3个雅可比矩阵：
Step 1: $x \rightarrow (a_1, a_2)$
$$
J_1 = \begin{pmatrix} \frac{\partial a_1}{\partial x} \ \frac{\partial a_2}{\partial x} \end{pmatrix}
$$
Step 2: $(a_1, a_2) \rightarrow (b_1, b_2)$
$$
J_2 = \begin{pmatrix} \frac{\partial b_1}{\partial a_1} & \frac{\partial b_1}{\partial a_2} \ \frac{\partial b_2}{\partial a_1} & \frac{\partial b_2}{\partial a_2} \end{pmatrix}
$$
Step 3: $(b_1, b_2) \rightarrow p$
$$
J_3 = \begin{pmatrix} \frac{\partial p}{\partial b_1} & \frac{\partial p}{\partial b_2} \end{pmatrix}
$$
根据链式法则(Chain Rule via Matrix Multiplication)：
$$
\frac{dp}{dx} = J_3 \cdot J_2 \cdot J_1
$$

Code

手动计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
import torch
import torch.nn as nn
from torch.autograd.functional import jacobian

# 设置随机种子便于复现
torch.manual_seed(0)

# 1. 定义 1-2-2-1 的 MLP
class SmallMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.l1 = nn.Linear(1, 2)  # x -> a 
        self.l2 = nn.Linear(2, 2)  # a -> b 
        self.l3 = nn.Linear(2, 1)  # b -> p 
        self.act = torch.tanh      # 隐藏层激活函数

    def forward(self, x):
        a = self.act(self.l1(x))
        b = self.act(self.l2(a))
        p = self.l3(b)            
        return p

model = SmallMLP()

# 选一个标量输入 x0
x0 = torch.tensor([1.0])  # shape: (1,)

##########################################
# 2. 定义 3 个“连接过程”的函数
##########################################

# x -> a
def layer1(x):
    # x: shape (1,)
    a = model.act(model.l1(x))
    return a  # shape (2,)

# a -> b
def layer2(a):
    b = model.act(model.l2(a))
    return b  # shape (2,)

# b -> p
def layer3(b):
    p = model.l3(b).squeeze()  # 变成标量张量 shape ()
    return p

# 整体映射 x -> p
def whole(x):
    a = layer1(x)
    b = layer2(a)
    p = layer3(b)
    return p  # 标量

##########################################
# 3. 计算 3 个雅可比矩阵 J1, J2, J3
##########################################

# J1 = d a / d x, shape: (2, 1)
J1 = jacobian(layer1, x0, create_graph=False)  # 输出 shape 为 (2, 1)

# 计算 J2 时需要在当前 x0 下的 a 值
a0 = layer1(x0).detach()
J2 = jacobian(layer2, a0, create_graph=False)  # shape: (2, 2)

# 计算 J3 时需要当前 a0 对应的 b 值
b0 = layer2(a0).detach()
J3 = jacobian(layer3, b0, create_graph=False)  # shape: (1, 2)

print("J1 (d a / d x) shape:", J1.shape)
print(J1)
print("J2 (d b / d a) shape:", J2.shape)
print(J2)
print("J3 (d p / d b) shape:", J3.shape)
print(J3)

##########################################
# 4. 直接对整体网络求 d p / d x
##########################################

dp_dx = jacobian(whole, x0, create_graph=False)  # shape: (1,)
print("dp/dx (from whole network):", dp_dx)

##########################################
# 5. 验证 dp/dx = J3 * J2 * J1
##########################################

# 需要把 J1, J2, J3 reshape 成标准矩阵形状:
# J1: (2, 1)  已经是矩阵
# J2: (2, 2)  已经是矩阵
# J3: (1, 2)  已经是矩阵
J1_mat = J1        # (2, 1)
J2_mat = J2        # (2, 2)
J3_mat = J3        # (1, 2)

# 矩阵乘法：1x2 @ 2x2 @ 2x1 -> 1x1
dp_dx_chain = J3_mat @ J2_mat @ J1_mat
print("dp/dx from J3*J2*J1:", dp_dx_chain)

# 两者数值比较
print("difference:", dp_dx_chain.item() - dp_dx.item())
1
2
3
4
5
6
7
8
9
10
11
J1 (d a / d x) shape: torch.Size([2, 1])
tensor([[-0.0040],
        [ 0.5156]])
J2 (d b / d a) shape: torch.Size([2, 2])
tensor([[-0.2704,  0.1882],
        [-0.0139,  0.5565]])
J3 (d p / d b) shape: torch.Size([2])
tensor([-0.2137, -0.1390])
dp/dx (from whole network): tensor([-0.0609])
dp/dx from J3*J2*J1: tensor([-0.0609])
difference: 0.0

使用自动微分

1
2
3
4
5
6
7
8
9
10
11
12
# 1. 构造需要求导的输入 x
x = torch.tensor([1.0], requires_grad=True)  # shape: (1,)

# 2. 前向传播得到标量输出 p
p = model(x)          

# 3. 对 p 反向传播
p.backward()

# 4. 此时 x.grad 就是 dp/dx
print("dp/dx (from autograd backward):", x.grad.item())
print("difference:", x.grad.item() - dp_dx.item())
1
2
dp/dx (from autograd backward): -0.060868293046951294
difference: 0.0