Note

在FB-PINN中，问题域$\Omega \subset \mathbb{R}^d$被细分为$n$个重叠的子域$\Omega_i \subset \Omega$，子域的细分可以为任意类型，规则或不规则，且可以有任何重叠宽度（但子域之前有重叠是必须的）。简单起见，我们展示一种规则细分（超矩形划分）：

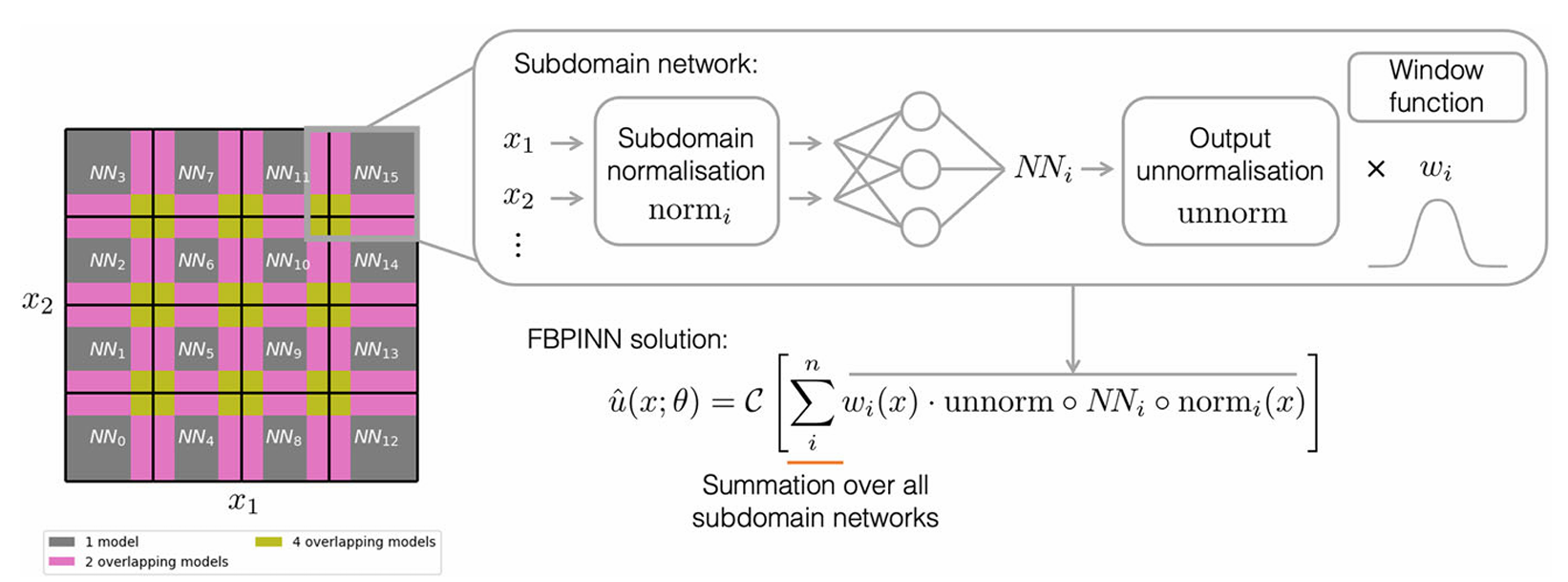
我们有近似解：
$$\hat{u}(x;\theta) = \mathcal{C}\left[ \overline{NN}(x;\theta) \right]$$
这里$x \in \Omega \subset \mathbb{R}^d$，物理坐标；$\overline{NN}(x;\theta)$是把所有子域网络加一起的函数；$\mathcal{C}$是约束算子，用于硬边界

其中：
$$
\overline{NN}(x;\theta) = \sum_{i}^{n} w_i(x) \cdot \text{unnorm} \circ NN_i \circ \text{norm}_i(x)
$$
$NN_i(x;\theta_i)$是置于每个子域$\Omega_i$中的独立神经网络，对于每个$NN_i$：

  1. 对输入进行归一化$\text{norm}_i(x)$，把输入$x$转换为$x \in [-1,1]$
  2. 进入子域网络$NN_i$
  3. 统一输出“反归一化”$\text{unnorm}$，确保每个子域网络的输出保持在$[-1,1]$范围内
  4. 窗口函数$w_i(x)$，把网络限制在子域

$NN_i$可以使用任何神经网络，简单起见只考虑MLP

$w_i(x)$在子域外部值几何为0，在子域内大于0，规则超矩形划分（1D是一维区间，2D是很多小矩形），采用以下窗口函数：
$$
w_i(x) = \prod_{j}^{d} \phi\left( \frac{x^j - a_i^j}{\sigma_i^j} \right) \phi\left( \frac{b_i^j - x^j}{\sigma_i^j} \right)
$$
$j$表示输入向量的每个维度，$a_i^j$和$b_i^j$表示每个维度中左右重叠边界（$a_i^j < b_i^j$），$\phi$是sigmoid函数，$\phi(x) = \frac{1}{1+e^{-x}}$，$\sigma_i^j$是控制斜率的参数，使得窗口函数在重叠区域外几乎为0。

最终，FB-PINN使用无约束损失函数：
$$
\mathcal{L}(\theta) = \mathcal{L}p(\theta) = \frac{1}{N_p} \sum{i}^{N_p} \left| \mathcal{D}\left[ \hat{u}(x_i;\theta); \lambda \right] - f(x_i) \right|^2
$$

Experiments

为了把上述方法进行实践，我们同样考虑之前的一维示例：
$$\frac{du}{dx} = \cos(\omega x),$$ $$u(0) = 0,$$
这个方程有精确解：
$$u(x) = \frac{1}{\omega} \sin(\omega x)$$
我们假设解为：
$$\hat{u}(x; \theta) = \tanh(\omega x) NN(x; \theta)$$
这里$\tanh(\omega x)$就是约束算子$\mathcal{C}$

在低频情况下，域$x \in [-2\pi, 2\pi]$被划分为$n=5$个重叠子域，每个子域之间的重叠区宽度为1.3。为了获得5个子域，我们首先将计算域分为5个等距点：

1
2
3
4
5
6
import numpy as np

xmin, xmax = -2*np.pi, 2*np.pi
n_sub = 5
centers = np.linspace(xmin, xmax, n_sub) 
centers # array([-6.28318531, -3.14159265, 0. , 3.14159265, 6.28318531])

完整子域的长度由不重叠区宽度与重叠区宽度组成

1
2
3
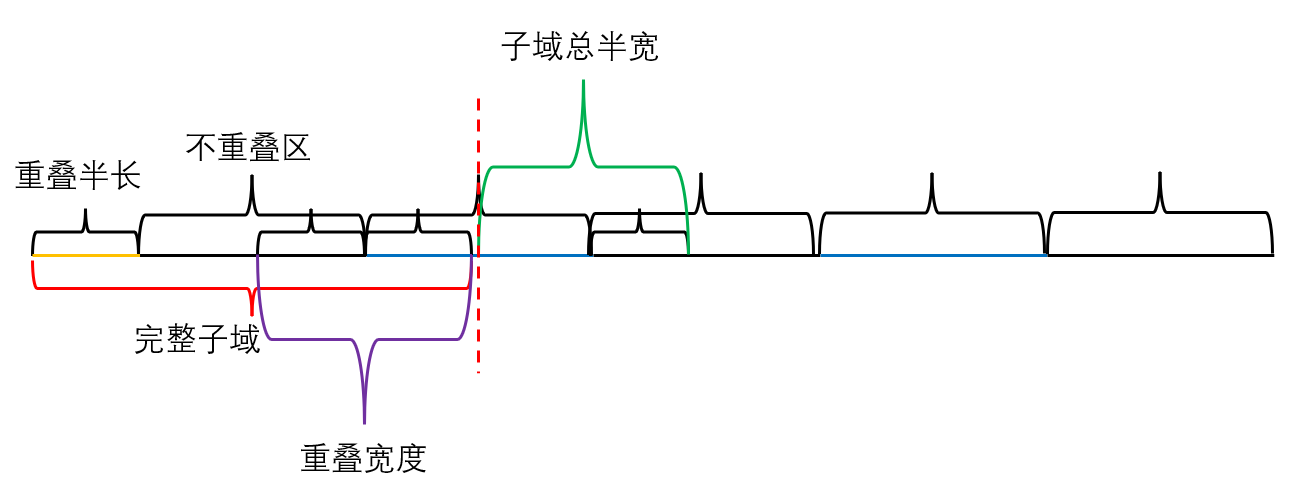
4
base_width = (xmax - xmin) / n_sub   # 不重叠的宽度  4*np.pi/5 = 2.5132741228718345
overlap = 1.3                        # 重叠区宽度 overlap 宽度=1.3
half_width = base_width/2 + overlap/2   # 子域总半宽 = non-overlap/2 + overlap/2
half_width # 1.9066370614359172

有了子域总半宽，要构建5个子域自然是5个等距点各自左右取一个子域总半宽，我们可以得到每个子域的左边界，右边界坐标：

1
2
3
4
5
6
7
import torch
# 每个子域的 [left, right]
sub_lefts  = torch.tensor([c - half_width for c in centers], dtype=torch.float32)
sub_lefts # tensor([-8.1898, -5.0482, -1.9066, 1.2350, 4.3765])

sub_rights = torch.tensor([c + half_width for c in centers], dtype=torch.float32)
sub_rights # tensor([-4.3765, -1.2350, 1.9066, 5.0482, 8.1898])

每个子域的总长度为：（2.51 + 1.3 = 3.81）

1
sub_rights -  sub_lefts # tensor([3.8133, 3.8133, 3.8133, 3.8133, 3.8133])

为了给每个子域设置一个单独的网络，可以如下构建模型序列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import torch.nn as nn

class SubNet(nn.Module):
    def __init__(self, in_dim=1, out_dim=1, width=16, depth=2):
        super().__init__()
        layers = [nn.Linear(in_dim, width), nn.Tanh()]
        for _ in range(depth - 1):
            layers += [nn.Linear(width, width), nn.Tanh()]
        layers += [nn.Linear(width, out_dim)]
        self.net = nn.Sequential(*layers)

    def forward(self, x):
        return self.net(x)

subnets = nn.ModuleList([SubNet(width=16, depth=2) for _ in range(n_sub)])

模拟结果：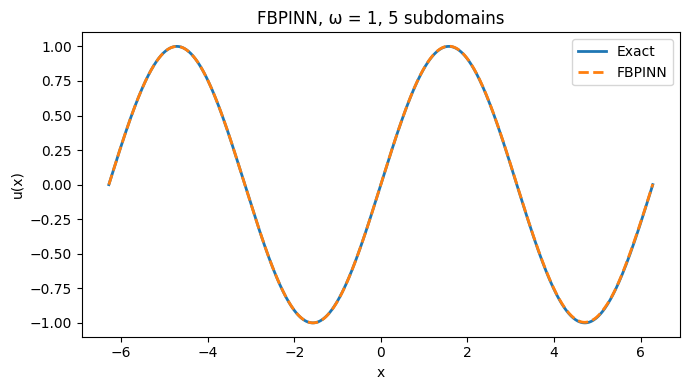

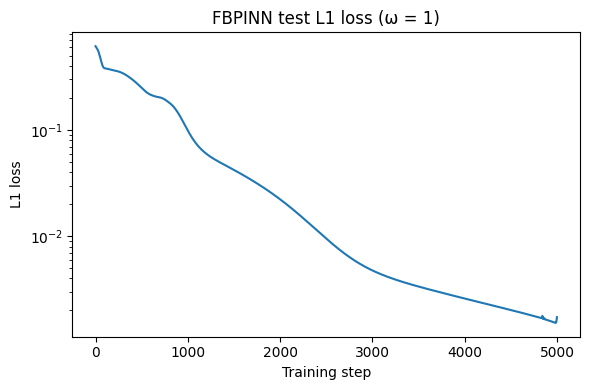
窗口函数的可视化：

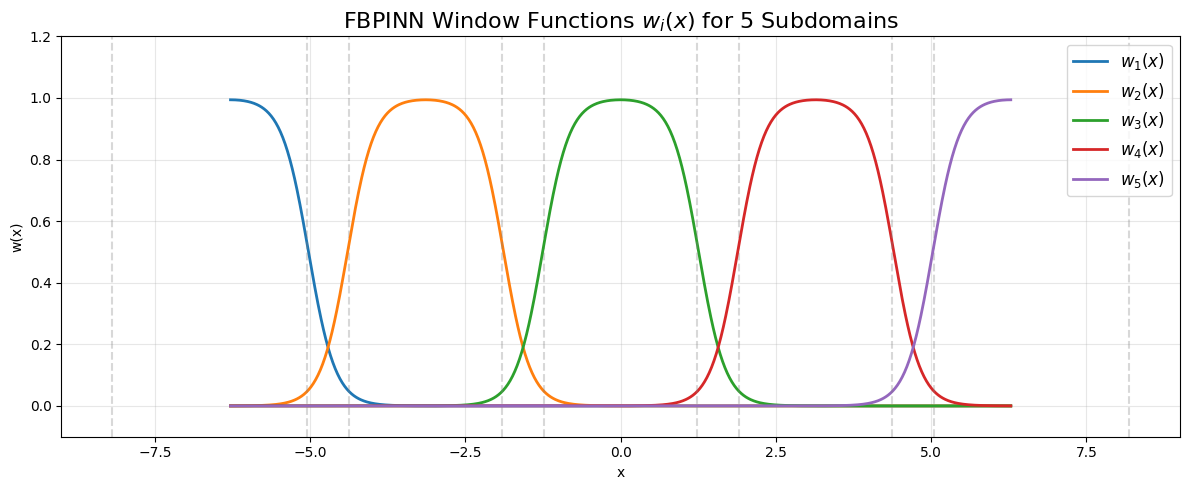
合起来：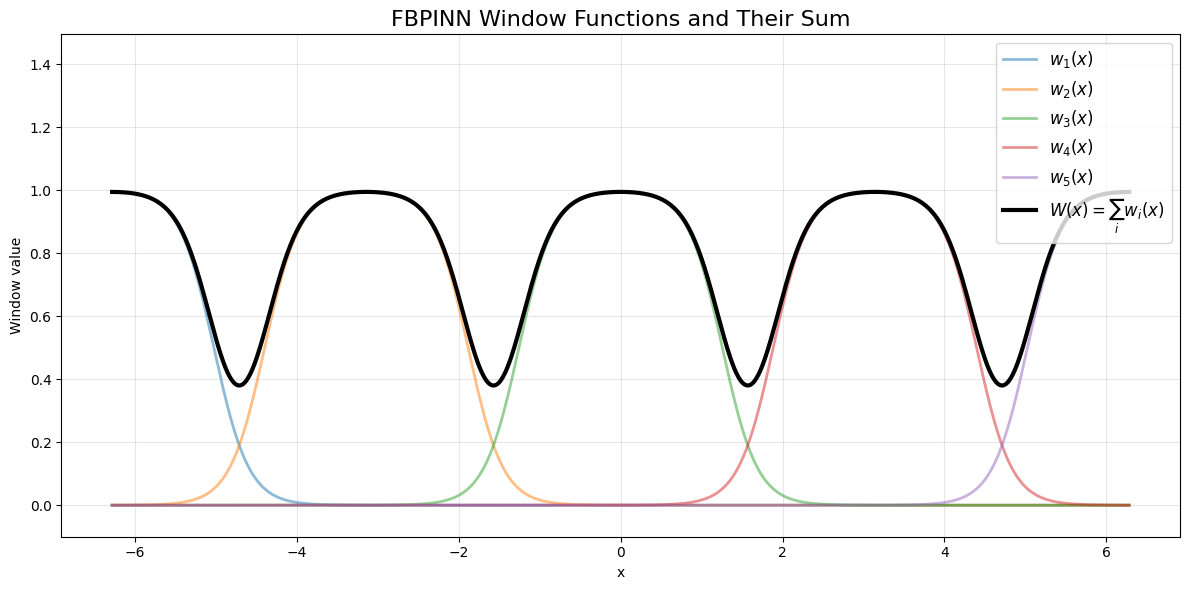

对于上述问题，向更高频率扩展等同于向更大的域尺寸扩展，因为我们在将输入变量输入网络之前，已经将其在域内归一化到$[-1,1]$，所以保持$\omega=1$不变，同时将域尺寸扩大15倍并重新归一化，这给神经网络带来的优化问题与将$\omega$改为15的情况相同。

对$\omega$为15时，我们构造30个子域，重叠宽度为0.3，同样采取2个隐藏层，每层16个神经元的简单网络，残差点扩充为3000，训练次数扩充为10000 epochs：

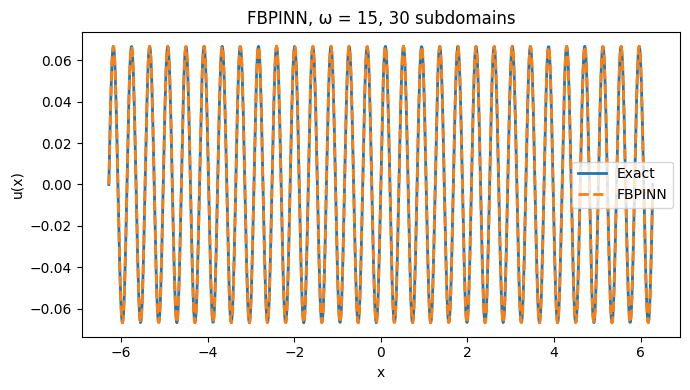
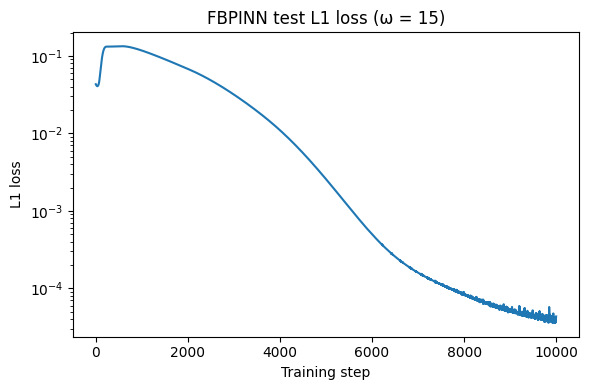
效果比之前没用FB方法的复杂的多的网络效果好很多

每个子网络的输出显示如下：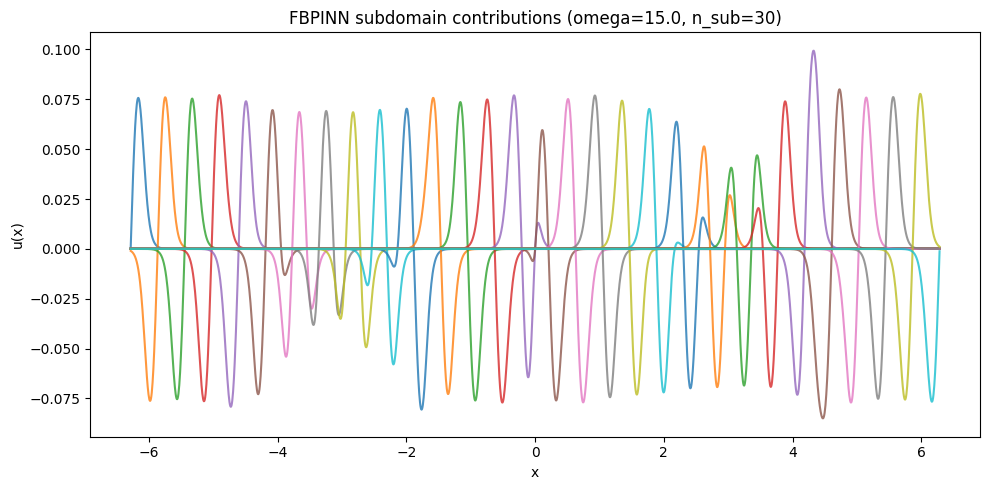

完整代码在srrdhy/FB-PINN-

Reference

Finite basis physics-informed neural networks (FBPINNs): a scalable domain decomposition approach for solving differential equations | Advances in Computational Mathematics